Нужна ли математика на пасеке?

 Чем может быть полезна пчеловоду на пасеке математика?  Ну вот и подошел к концу медосборный сезон 2014 года. Среди пчеловодов-любителей есть множество таких, которые сетуют на судьбу и довольствуются 20-30 кг меда, полученными от каждой семьи в те-чение сезона. Небольшое количество пчеловодов (и таких в Украине 6-7 тыс. человек) ежегодно получают от своих пчелосемей по 50-60 меда от каждой. Они, как правило, держат по 80-100 пчелосемей и сдают специализированным предприятиям по 5-6 тонн ежегодно. Но есть совсем небольшая группа пчеловодов 300-500 человек (может, и больше), которые от каждой семьи получают по 100-120 кг меда. У них, как правило, улья большеобъемные – по 30 и более рамок в пересчете на стандартную рамку 435 Ч 300 мм. У них пчелы никогда не слетают и не гибнут. Это пчеловоды от Бога. Они чисто интуитивно (на подсознательном уровне) познали для себя закон образования и развития пчелосемей и за долгие годы работы с пчелой достигли вершины мастерства, и по праву считаются мастерами своего дела, что мы еще называем искусством пчеловождения.
 
 За мою 14-летнюю практику мне неоднократно приходилось сталкиваться со всеми вышеозначенными категориями пчеловодов. При личной беседе, по телефону или письменно я пытался выяснить у них интересующие меня вопросы. На многие вопросы они давали четкие, исчерпывающие ответы. Но вот некоторые вопросы оста-ются без ответа и по сегодняшний день, причем нет на них ответа и в официальной литературе. А если ответ и есть, то эти ответы, как правило, даются в расплывчатой (обтекаемой) форме, по которой невозможно иметь четкого представления о сути рассматриваемого явления. Например: – биологически сложившиеся размеры пчелиного жилища; – биологический предел яйценосткости матки и множество других примеров. Мой вопрос «Почему во время обильного взятка отдельные пчелосемьи во все пустые ячейки заносят пыльцу, а не заливают нектаром, как и положено им это делать?» ставит моих собеседников в тупик. Нет, ответы есть, но они не менее расплывчатые, чем выше-означенные. По крайней мере, как сделать так, чтобы вместо пыльцы пчелы стали активно носить нектар, мне так никто не ответил.
 
 Изучив еще тогда (13-14 лет назад) огромное количество учеб-ной литературы по пчеловодству, я все больше и больше убеждался в том, что созданная учеными-пчеловодами теория о жизни семей медоносных пчел только описывает круг наблюдаемых явлений, что не позволяет вскрыть сути изучаемого процесса, да и не позволяет делать никаких прогнозов. Но ведь наукой считается та область человеческих знаний, где все процессы, составляющие предмет ее изучения, не только уста-новлены, изучены, объяснены и описаны, но и при помощи законов, найденных этой наукой, мы можем не только вскрывать суть этих процессов, но и предсказывать дальнейших ход этих процессов. Следовательно, нынешняя наука о пчеле по сути является экспериментально-описательной и все выводы ее базируются ис-ключительно на системе умозрительных построений, но нельзя же одними лишь чувствами, словами или же умозаключениями познать законы Природы. Так и найдя ответов на многие интересующие меня вопросы, я решил блеснуть перед новыми моими коллегами своими познани-ями в математике. Это было в конце июня 2000-го года. Мы тогда только переехали к огромному массиву подсолнечника. Уже тогда я пытался, пусть и визуально, дать количественную оценку состояния своим 7-ми семьям (для этих целей я позднее купил почтовые весы).Так, в моем дневнике появилась запись 

А потом, как учили в школе, на координатной плоскости по точ-кам я начертил график, который изображен на рис. 1  
 
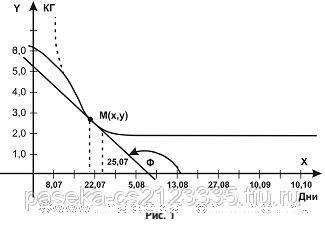
 Далее. Для выяснения характера кривой я на искомой кривой выбрал произвольную точку М с текущими координатами x и y. Через данную точку М (х; у) провел касательную к данной кривой, которая пересекла ось ОХ под углом φ, как указано на рис. 1. Следовательно, если связать уравнением координаты (x; y) точки М с углом φ наклона касательной, можно получить аналитическое выражение изучаемой кривой линии на определенном временном промежутке. Например, с 15.07 по 10.10. А так как такого типа задачи есть практически в любом учеб-нике математического анализа, то я приведу только краткое ре-шение задачи. Угловой коэффициент касательной к кривой в данной точке М (x; y), как известно, равен значению производной функции в этой точке, поэтому: – у/х = dy/dx: у/х – тангенс угла j, но в нашем случае необхо-димо брать тангенс угла (π – j), а не угла j. Поэтому tg(π – j) берем отрицательный. А далее, интегрируя наше выражение, получаем: 

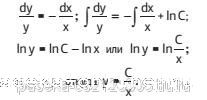
Постоянная интегрирования С легко находится из начальных условий, а вот заменить переменную х на время t занятие довольно хлопотное, и поэтому я не буду задерживать внимание пчеловодов на дальнейших подробностях.
 
 Тем более, что эту же задачу я уже рассматривал в журнале «Украинский пасечник» №№ 4, 9, 12 за 2006 год и в № 7 за 2007 год, так что если есть желание рассмотреть данный вопрос подробнее, то необходимо прочесть эти журналы, и в особенности «УП» №9 за 2006 год, стр. 16-20. Итак, как видно из рис. 1, характер поведения кривой (аналити-ческое выражение функции) в период времени с 10-12 июля и по 15 октября можно выразить формулой у = C/х, а это часть положитель-ной ветви гиперболы, где C – это наличие условия, а переменную х нужно представить как функцию от времени t, т.е. х = j(t).
 
 Я понимал, что мой закон примитивный и не отображает все процессы, протекающие как в самой пчелосемье, так и за ее пределами, но все же я решился показать найденный мной закон своим новым коллегам по пчеловодству. Но они, только услышав о производной, дифференциале, интеграле, шарахались от моего закона во все стороны, словно от чумы. А один из них так и заметил: «Наші діди бджіл тримали, мед качали та ніяких формул не знали. І так у всі віки» А другой добавил: «У пчеловода формула одна – талант, тер-пение и трудолюбие. И лет эдак через 7-10 ты достигнешь вершин мастерства». Вот и вся пчеловодческая философия.
 
 Тогда я еще не понимал, что искусством пчеловождения, в прин-ципе, овладевает небольшая группа пчеловодов-практиков, т.е. веду-щая рациональное пчеловождение, и которая подразумевает пчело-водство в неразрывной связи с его материальной составляющей, т.е.: «Больше мёда – больше пчёл; больше пчёл – больше мёда». Например, весной, после очистительного облёта дай каждой семье по 12-15 кг мёда и по 2-3 рамки с пергой, и уже через 40-50 суток подвози пчел к цветущему медоносу и черпай мёд лопатой, что вобщем-то и спра-ведливо. Да и многовековой опыт это подтверждает. Вот если бы не докучливое роение, порой срывающее все планы пчеловода, да чуть ли не ежегодная гибель сотен тысяч пчелосемей зимой, был бы самый настоящий пчеловодный рай…
 
 Но вот уже лет 200 эти две задачи ученым биологам оказались «не по зубам». По крайней мере пресловутая «тайна дупла» не раскрыта и по сегодняшний день. Она и не может быть раскрыта при ущербных познаниях господ-биологов в физике и математике. А физика и математика позволяют отвлечься от материальной составляющей любых процессов, протекающих как в природе, так и в живой материи (математики говорят ещё – абстрагироваться), и уже при помощи законов, методов математики и физики можно разрешить любую задачу.
 
 Например: еще в 1826-м году немецкий физик Георг Ом открыл свой знаменитый закон: сила тока в проводнике пропорциональна разности потенциалов на концах проводника и обратно пропорци-ональна сопротивлению данного проводника – словесное описание закона: I = V/R – буквенно-символьная запись закона или аналити-ческая запись закона (формула). Но не все пчеловоды знают, что при помощи данного закона можно решать задачи и в теплотехнике, т.е. данный закон можно применить и при решении задач с дуплом, где живут пчёлы, немного его модернизировав. За разность потенциалов можно взять разность температур, т.е. температуры наружного воздуха и температуры внутри дупла. Например, –40 °С и + 6 °С.
 
 При этом необходимо учесть, что внутри дупла имеется источник тепла (тепловой энергии), которую генерирует пчелиный клуб, поэтому эти два тепловых потока непременно где-то встретятся – практически от данной границы холод/тепло и зависит судьба пчелиного клуба (в электротехнике эта граница носит название – узел таков) и здесь же необходимо учесть еще, что передача тепла происходит путем отдачи тепла телом с более высокой температурой к телу с более низкой температурой, и когда решение уравнения станет отрицательным (положительным), то это и будет граница холод/тепло.
 
 Например: если эта граница холод/тепло проходит внутри стенки дупла, то, как говорят сейчас пчеловоды, пчёлы клуба чувствуют себя комфортно, т.е. в дупле сравнительно тепло и влажно. Если граница холод/тепло проходит по внутренней стенке дупла, то она всегда мокрая (как иногда в холодной комнате – стена постоянно сырая). В таком дупле холодно и сыро, и влажность около 100 %. Если граница холод/тепло проходит внутри объема дупла, то в таком дупле при морозе на стенках всегда изморозь, а при дли-тельной оттепели изморозь тает и стенки дупла мокрые. Что тоже не очень хорошо.
 
 Для нахождения сопротивления протеканию теплового потока через стенку дупла необходимо знать геометрические размеры самого дупла и воспользоваться справочными данными по тепло-проводности материалов (коры дерева, древесины, воздуха и т.п., а для нахождения тепловой энергии пчелиного клуба еще необходимо составить уравнение теплового баланса, после чего, решив систему уравнений, можно будет найти общий расход горючего (мёда) пче-линым клубом для поддержания теплового режима дупла. Поскольку типовые задачи приводятся практически во всех учебниках по физике в разделах теплотехники, поэтому я здесь не буду приводить самого решения, так как это не только долго и утомительно, но и лимитирует меня во времени. А просто замечу, что ещё зимой 2001-2002 гг. я получил решение данной задачи по модели идеального дупла (см. рис. 2), при котором выяснилось, что пчелиный клуб в модели идеального дупла сжигает за долгих 6 месяцев всего 1,8-2,2 кг мёда, если мёд принимать идеально чистым, т.е. содержание неперевариваемых остатков в мёде не должно превышать 2%.
 
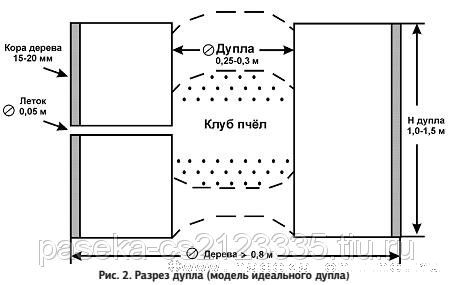
 Таким образом, сама природа побеспокоилась о своих питом-цах, поселив их в дупле дерева, где позволила им экономно рас-ходовать свои кормовые запасы и практически не изнашиваться за долгих 6 месяцев.  При нынешнем многообразии теплоизоляционных материалов пчеловоду легко устроить жилище пчёл по типу дупла, но при этом все пчеловоды совершают ошибку. Забывают об открытом настежь летке, легко переходя через который холодный воздух чуть ли не мгновенно охлаждает внутреннюю полость улья и ваши усилия по теплоизоляции улья оказываются напрасными. Следовательно, для того, чтобы достичь эффекта дупла, необхо-димо не только теплоизолировать сам корпус улья, но и сам леток, т.е. сделать леток-вкладыш, как предлагает В. Паращинец (см. «УП» №6 за 1994 год, «Пасека» №8 за 2001 год).
 
 Так как теплоизоляционные материалы очень дорого стоят, да и сама процедура закрепления теплоизоляции на улье очень трудоемкая, то большинство пчеловодов пошло по более легкому пути: укрывают своих питомцев под легким навесом, закрытым со всех сторон толью (рубероидом) и другими дешевыми материалами, таким образом, ограждая своих пчел от воздействия агрессивной внешней среды, занося туда своих питомцев после установившихся холодов (в конце ноября – начале декабря). Зимуют пчёлы под таким укрытием вполне удовлетворительно с расходом меда, не превышающем 6-7 кг на семью. Единственный недостаток зимовки пчел под легким укрытием – необходимо всю зиму бороться с грызунами, они лезут отовсюду.
 
 Отдельно необходимо сказать о вентиляции дупла. Здесь необ-ходимо вспомнить, что пчёлы – это насекомые, которые появились на земле в эпоху каменноугольного периода вместе с хвойными деревьями порядка 250 млн. лет назад. Тогда в атмосфере Земли кислорода было мало – порядка около 0,2-0,3%, а содержание углекислоты доходило до 5-7% (см. Камшилов М.М. «Эволюция биосферы», М: 1973; стр. 66-67). Поэтому воздух в дупле с повышенным содержанием СО2и по-нижением содержания О2 для пчёл – привычное дело, как и для их далёких предков. Но дело даже не в этом, а в том, что расходуя до 4 кг мёда за 6 месяцев, в результате окислительно-восстановительной реакции в месяц менее 0,5 л. воды, т.е.: 4000/6 Ч 0,7 = 470 г. воды. А это около 15 г воды в сутки, часть из которой используется пчёлами для своих нужд и совсем небольшая часть паров воды за счет раз-ности парциальных давлений водяных паров наружного воздуха и водяных паров воздуха, содержащегося в дупле, сравняется через леток, словно вода по сообщающимся сосудам, ведь парциальное давление паров воды во внутреннем объёме дупла будет больше, чем парциальное давление паров воды наружного воздуха. И си-стема, таким образом, стабилизируется или, что же, – равновесие системы: наружный воздух – воздух дупла, – восстановится.

 Для справки.Состав нынешнего воздуха (сухого): азот N – 78 %, кислород О2– 20,95 %, аргон А2– 0,93 %, углекислый газ СО2 – 0,03 %, другие газы – 0,09 %. Как известно, эти газы между собой химически не взаимодей-ствуют, поэтому у каждого из них своё частичное (парциальное) давление и, если какой-либо из этих газов исчезает (например О2 в дупле при сжигании мёда), то на смену ему из атмосферы (резерва) непременно по летку поступит О2из атмосферы, как вода в сооб-щающихся сосудах. Но при этом необходимо учитывать сопротивление стоячего воздуха в летке, которое (сопротивление) и будет зависеть от диа-метра и длины летка, от расположения зимнего клуба по отношению к летку; от температуры наружного воздуха и тем-пературы воздуха внутри дупла, т.е. от разницы этих температур в каждый момент времени и др. причин.
 
 И состав воздуха в дупле будет отличен от атмос-ферного, так как он (воздух) находится в постоянном объеме, т.е. объём дупла практически неизменен: V дупла = consta, а объём атмосферы безграничен (объём дупла увеличивается на объём сжигаемого мёда). Всё это можно просчитать, если знать матема-тику, физику, химию и др. науки. Но так как пчеловоды (как и биологи) в своей основе не очень дружат с этими науками, то лет десять тому назад у меня и возникла идея создать математику для пчеловодов, да и не только. Ведь математику знает и понимает ограниченное число людей на земном шаре. От этого страдает не только пчеловодство, но и биология в целом, и другие науки. Ведь зная суть рассматриваемого явления, мы не только глубже познаём все процессы, происходящие в данном явлении, но и в конечном итоге уже можем управлять этим явлением.
 
 Так, например, все пчеловоды знают, что матка зароившейся семьи перед запечатыванием первого маточника полностью прекращает яйцекладку и та-ким образом рабочие пчёлы подготовили ее к вылету с роем-перва-ком. Если теперь каким-либо образом матку заставить откладывать яйца, то она не сможет покинуть семью с роем-перваком. Но это и есть управление процессом роения, и у пчеловода появляется дополнительная возможность распоряжаться даль-нейшей судьбой зароившейся семьи до выхода первой молодой матки. А если вы уничтожите все маточники, и при этом старая матка будет продолжать откладывать яйца, то при определён-ных условиях семью удается вывести из роевого состояния. Точно так происходит и в матема-тике – если вы не знаете арифметики, то вам никогда не освоить и алгебры, а если вы знаете арифметику и тем более, если вы кое-что помните из школьного курса по алгебре, то как раз вас я и приглашаю вместе со мной изучить ма-тематику для пчеловодов и не только.
 
 Но это уже тема для другого разговора. А для скептиков, которые отмахиваются от математиков, словно от на-зойливых мух, я приведу одно из своих «ноу-хау», которое вот уже 12 лет я применяю в своей повседневной пчеловодческой практике. В результате поисков и действий, о которых я говорил выше, мне удалось  установить, что пчелиная семья массой m = 2,5 кг на день весеннего облёта и имеющая яйцекладущую матку (порядка 2000 яиц в сутки уже на 54 день своего развития после очистительного облёта) может занять полностью 20-рамочный улей-лежак на низко-широкую рамку (435 Ч 300 мм) и в связи с избытком пчёл-воспитательниц (кормилиц) уже может отстраивать первые мисочки на боковых и нижних рёбрах гнездовых рамок (сотов), что хорошо видно на приведённом рис. 3.
 
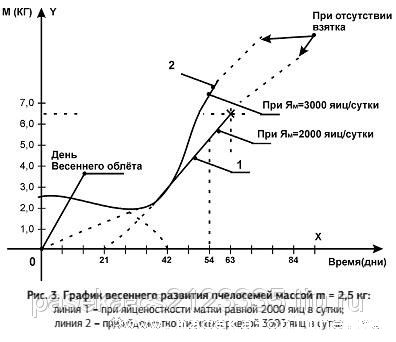
 Для упрощения вычислений график построен без учёта яиц, отложенных маткой до дня весеннего облёта; – продолжительность жизни зимовалой пчелы условно принята ≤ 42(± 7 суток); – продолжительность жизни пчелы весенней генерации условно принята ≤ 42(+ 3–15 суток); – вместимость улья условно принята за 5 кг массы пчелы, т.к. 20 рамок Ч 0,25 кг = 5 кг. Из этого графика отчётливо видно, что для всех пчелосемей с начальной массой m = 2,5 кг на день очистительного облёта и яйце-кладущей маткой от Ям= 1200 яиц/сутки и до Ям = 3000 яиц/сутки первое расширение гнезда необходимо проводить не ранее, чем 42 суток при условии, естественно, что матка не откладывала яиц до весеннего облёта. На основании моих многолетних наблюдений было установлено, что именно так в вышеобозначенных семьях и происходит, т.к. видно на графике, т.е. не позднее 54-го дня после очистительного облёта в 20-рамочных ульях-лежаках у семей с на-чальной массой m = 2,5 кг и яйцекладущей маткой Ям= 2000 яиц/ сутки появляются свежеотстроенные роевые мисочки различного цвета, а у семей, где имелись яйцекладущие матки более 2000 яиц в сутки, еще ранее (см. рис. 3 линия 2).

 Таким образом, зная биологические законы пчелосемей, исполь-зуя математику и физику, можно легко построить графики весен-него развития пчелосемей массой m = 0,5 кг и до m = 3,5 кг живой массы пчелы на день весеннего облёта и, в зависимости от объёма улья, величины яйценосткости матки и поступления нектара, легко определяется дата отбора пчёл при создании отводков и, что самое интересное, данные графика очень точно согласуются с «правилом седьмой рамки» Г.Ф. Таранова, согласно которому многие пчеловоды и формируют отводки от основных семей. 

Овчатов В.А., г. Каменка-Днепровская, Запорожская обл.  Источник: Песечный Вестник № 9’ 2014